非従来型超伝導体中の局所的超伝導状態

[1] Y. Iguchi et al., Physical Review B 103, L220503 (2021).

[2] I.P. Zheng, Y. Iguchi, et al., Physical Review B 100, 024514 (2019).

1. 孤立した超伝導Vortexの動的応答を可視化

　走査型SQUID顕微鏡は局所的な磁束と帯磁率を観測する事ができるため、Vortex磁場の観測およびその動的応答を直接観測する事ができる。我々は低温で双晶化する事が知られている超伝導体FeSeにおいてVortex動力学の直接的観測を初めて行い、双晶境界線に沿った異方的なピン止めポテンシャルの存在を可視化することに成功した。[2]

　また、圧力中で双晶化する事が知られている重い電子系超伝導体URu$_2$Si$_2$においても同様に測定を行い、局所的に異方的・等方的なピン止めポテンシャルを持つことが分かった。[1] ここで観測された異方的なピン止めポテンシャルはFeSeで観測されたもののように長距離に渡って直線的に並んでいるわけではなくランダムに向いていることから、ここでは双晶化または電子のネマティック秩序による影響はほとんどなく不純物などの局所的な格子歪みが支配的であると考えられる。URu$_2$Si$_2$では等方的なピン止め力の温度依存性も初めて局所的に見積もっており、その温度依存性が$(1-(T/T_c)^2)^2$で表されることを示した。この結果は、このサンプルの不純物の大きさがおおよそ超伝導のコヒーレンス長程度であることを示唆している。

2.  カイラル超伝導候補物質URu$_2$Si$_2$における超流動密度と自発磁性の局所的な観測

    カイラル超伝導は非従来型超伝導体が自発的に時間反転対称性を破る角運動量を得る非常に興味深い量子現象である。これは非自明なトポロジカル状態であり表面もしくは欠陥付近に自発的なトポロジカルモード（例えばカイラルエッジカレントやマヨラナゼロモード）を持つと期待される。マヨラナゼロモードの観測はいくつかの超伝導体で報告されているが、カイラル超伝導については未だ決定的な証拠は報告されていない。 

   重い電子系超伝導体URu$_2$Si$_2$はカイラル（超伝導ギャップにノードを持つ時間反転対称性が破れた）超伝導の候補物質であり、また超伝導相と共存する隠れた秩序相の研究が長年に渡って精力的に行われてきた。しかし、ノード構造やカイラリティについては試料の質に依存しているため、本質的な超伝導状態については不明確である。本研究では、URu$_2$Si$_2$における自発的な磁性、局所超流動密度を観測するため、走査型SQUID顕微鏡を用いてミクロン単位でゼロ磁場下の磁束、低磁場による反磁性応答を測定した。[1]

    ２つのサンプルで超伝導相（$T_{SC}$=1.5 K）と共存する強磁性ドメイン（$T_{FM}$=16.1 K）を観測した。だが、強磁性ドメインから十分離れた超伝導相においてカイラル超伝導で期待させる自発的磁化は観測されなかった。この結果は、URu$_2$Si$_2$はカイラリティを持たないか検出可能な自発磁化を導かないことを示唆している。

　また、強磁性ドメインから十分離れた超伝導相において帯磁率のサンプル表面からの距離依存性からLondonの磁場侵入長を見積もり、その温度依存性を観測した。この結果から、線形の温度依存性を持つ超流動密度を観測した。これはURu$_2$Si$_2$における超伝導ギャップ中のノードの存在を示唆している。

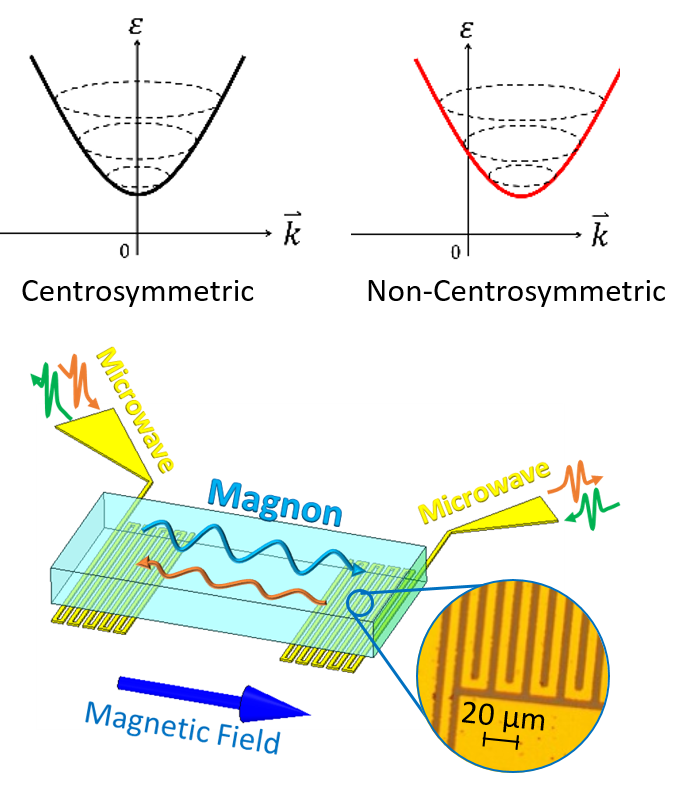
空間反転対称性が破れた強磁性体中のマグノンの非相反伝搬

[1] Y. Iguchi, S. Uemura, K. Ueno, and Y. Onose, Physical Review B 92, 184419(2015). 
(解説記事：井口雄介、小野瀬佳文、固体物理 vol.51 No.7(通巻605号)2016年 )

     相対論的ディラック方程式から導かれるスピン軌道相互作用は、空間反転対称性の破れた結晶においては、電子のバンド構造を変形、分裂させるなど大きな変形をもたらすことが知られている。その一つの例が、界面や極性物質などの系におけるラシュバ効果である。ラシュバ効果が起きるとバンド構造がスピン分裂を起こし、波数$+k$をもつ電子と$-k$を持つ電子のスピンが異なるようになる。実は、磁性体のスピン波励起（マグノン）においても類似した効果が観測される。空間反転対称性が破れた強磁性体では、ジャロシンスキー守谷相互作用とよばれるスピン軌道相互作用に由来した対称性に依存する相互作用が働き、それにより非対称なマグノンバンドが発現する。このときには、波数$+k$と$-k$のエネルギーが異なる非相反なマグノン伝搬が期待される。

　非対称バンド由来のマグノンの非相反伝搬は、これまで界面型（ポーラー型）ジャロシンスキー守谷相互作用が有限な薄膜中のみで観測が行われてきた。しかし、キラルなバルク強磁性体中で有限なキラル型ジャロシンスキー守谷相互作用においても非対称マグノンバンドが現れることが理論的に予想される。本研究では、キラルなバルク強磁性体LiFe$_5$O$_8$の単結晶試料と微細加工したマイクロ波アンテナを用いて、非相反なマグノン伝搬を観測した。[1]

　非対称バンド中では、高波数のマグノンにおいてより大きな非相反伝搬が期待される。また、低波数領域では磁気双極子相互作用を媒介とした静磁波モードが支配的で、マグノンバンドを対称に大きく変調する。このため我々は高波数マグノンを励起できる微細マイクロ波アンテナを作成した。このデバイス中で、マイクロ波の透過率として、ポート１から２、２から１へのマグノン伝搬を観測した。キラル強磁性体LiFe$_5$O$_8$中では、明らかな非相反性が観測されたが、反転対称強磁性体Y$_3$Fe$_5$O$_{12}$中では非相反性は見られなかった。また非相反マグノン伝搬の磁場方向依存性も観測した。この結果、キラル型ジャロシンスキー守谷相互作用由来の非相反性と静磁波モード由来の非相反性が区別できることを明らかにした。